Математика в жизни человека интересные факты ‒ сегодня рассказ пойдет именно об этом. Портал ФактыПро поможет разобраться в том, что же такое математика: что она из себя представляет и зачем нужна. Ведь очень часто многие говорят, что им математика не пригодится в жизни, потому что они будут поварами или лингвистами. Всё же такие люди очень сильно ошибаются. Математика нужна всем, к ней часто приходится обращаться даже в обычной повседневной жизни.
Математика в жизни человека
Математика ‒ является одной из основополагающих наук. Изначально она исследовала количественные отношения и пространственные формы. Если брать современное понимание, то это наука про отношения между объектами, о которых мало, что известно, кроме немногих их свойств. А именно тех, которые в качестве аксиом заложены в основании какой-либо математической теории.

Математика исторически сложилась на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке.

Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Она является фундаментальной наукой, предоставляющей средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.

Влияние математики на жизнь человека
В процессе изучения математики многих мучает вопрос: «Зачем им эта самая математика в жизни.» Ответ довольно прост. Ведь с нее все начинается в нашей жизни. Только ребенок родился и тут же появляются его первые цифры – вес и рост. С этого момента математика будет сопровождать человека шаг за шагом.
Регулярные занятия математикой способны развить мозг не хуже, чем физические упражнения развивают человеческое тело. Решение задач помогает расширить кругозор, а также повысить интеллект в целом.

Портал ФактыПро приведет несколько доказательств того, что занятие математикой дает хорошую пользу. Такие тренировки развивают мышление и память. Занятия математикой полезны для воспитания характера. При помощи математики люди учатся выстраивать причинно-следственные связи.
Математика и карьера
Математика влияет и на карьеру. И тут речь не об умении быстро считать. Важно общее развитие человека, которое обеспечивает изучение математики. В наше время успешная карьера очень зависит от знания точных наук.

Не зная математики крайне сложно работать в IT сфере. А это одно из передовых направлений нашего общества. При этом каждый программист обязан знать математические функции, чтобы успешно двигаться по карьерной лестнице. Отсюда можно сделать вывод. Математика – это основатель информационных технологий.

Без математики не обойтись даже юристу. Тренировки мозга помогают выстраивать более сложные комбинации для защиты или обвинения. Поэтому, получая дополнительное образование и знания, юристы становятся более креативными и высокооплачиваемыми.

Интересные факты о математике
Портал ФактыПро расскажет интересные факты о математике. Таких фактов безграничное количество, так как этой науке множество лет. Интересные факты про математику будут интересны даже детям. Вот некоторые из них:
- именно благодаря математике стало известно, что есть достаточно много способов завязать галстук, а именно – 177147;
- Альфред Нобель не включил математику в список наук за которые давалась премия (о причине этого споры идут до сих пор);
- есть даже известные писатели, которые были математиками, например, автор книги «Алиса в стране чудес» — Льюисс Кэрролл, был математиком.


Еще есть ряд таких фактов, которые будут интересны всем. Они не требуют объяснения, так как это просто факты:
- итальянцы не любят число 17;
- квадратные уравнения были придуманы очень давно, произошло это еще в 6 веке в Индии;
- с китайского число четыре в переводе означает «смерть».
Интересные факты про математику можно перечислять бесконечно, так как эта наука имеет очень далекие корни.
Математики и их открытия
Бесконечно можно говорить и о математиках с их открытиями, а также о вкладе в развитие современного мира. Таких математиков немало, притом в каждую эпоху.


Эвклид
Начнем с великого математика Эвклида. Он считается отцом-основателем геометрии. Он смог доказать много как теорем, так и гипотез. Научная деятельность Эвклида протекала в Александрии в III веке до н. э.
К сожалению, о личной жизни Эвклида сохранилось мало данных. Согласно преданию царь Птолемей, который захотел изучить геометрию, обратился за помощью именно к нему. До наших дней не дошло ни одного достоверного портрета ученого. Именно из-за этого все картины и скульптуры Эвклида являются просто плодами воображения.
Основное сочинение Евклида называется «Начала». Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако «Начала» Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино.
«Начала» состоят из тринадцати книг. Первая и некоторые другие книги предваряются списком определений. Первой книге предпослан также список постулатов и аксиом. В создании и развитии науки Нового времени «Начала» также сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.
Из других трудов Евклида до наших дней сохранились:
- Данные ‒ о том, что необходимо, чтобы задать фигуру;
- О делении ‒ сохранилось частично и только в арабском переводе; даёт деление геометрических фигур на части, равные или состоящие между собой в заданном отношении;
- Явления ‒ приложения сферической геометрии к астрономии;
- Оптика ‒ о прямолинейном распространении света.
- Поризмы ‒ об условиях, определяющих кривые;
- Конические сечения;
- Поверхностные места ‒ о свойствах конических сечений;
- Псевдария ‒ об ошибках в геометрических доказательствах (математические софизмы);
Евклиду приписываются также:
- Катоптрика ‒ теория зеркал; сохранилась обработка Теона Александрийского;
- Деление канона ‒ трактат по элементарной теории музыки.

Пифагор
Следующим, о ком пойдет рассказ, станет – Пифагор. Его считают отцом всей математики. При этом не все историки согласны с тем, что именно он был родоначальником своей теоремы. Характерная для школы пифагористов особенность приписывать все открытия Пифагору, в сочетании с отсутствием письменной фиксации учения Пифагора до Филолая, делает реконструкцию первоначального учения весьма сложной задачей.
Пифагора можно назвать одним из самых известных математиков во всем мире. Он сделал весомый внос в развитие науки математики, а именно в геометрии.
Нумерология стала важной составляющей пифагореизма, приписываемой Пифагору. Идея о числовой сущности мира позволила разработать проект «оцифровки бытия», способствовала развитию математики. Нумерологию Пифагора сравнивают с идеей о том, что окружающий людей физический мир является «матрицей», в основе которой лежат числа. Внутри матрицы нет возможности увидеть числовую суть бытия. Числовая сущность мира доступна душе после смерти, после выхода из тела. Математика даёт возможность припомнить прежний опыт и постичь истинную реальность. В данном случае математика выступала основой метафизики. В данном случае математика вводила людей в заблуждение и использовалась не по назначению.
Согласно Аристотелю, пифагорейцы использовали математику для мистических, а не практических целей. Нечётные числа были мужскими, чётные — женскими, цифра пять представляла брак, так как была суммой двух и трёх.
«Идеальным числом» пифагорейцы считали десятку, стараясь не собираться группами более десяти человек. Тетрактис был для них символом, в котором они усматривали музыкально-числовую структуру космоса.
Заслуга пифагоровой нумерологии состоит в том, что наука о числах была выведена за пределы употребления в торговле.
В математике с именем Пифагора связаны систематическое введение доказательств, дедуктивное построение геометрии прямолинейных фигур, создание учения о подобии, построение некоторых правильных многогранников и многоугольников, учение о чётных и нечётных, простых и составных числах, о пропорциях, об арифметических, геометрических и гармонических средних.
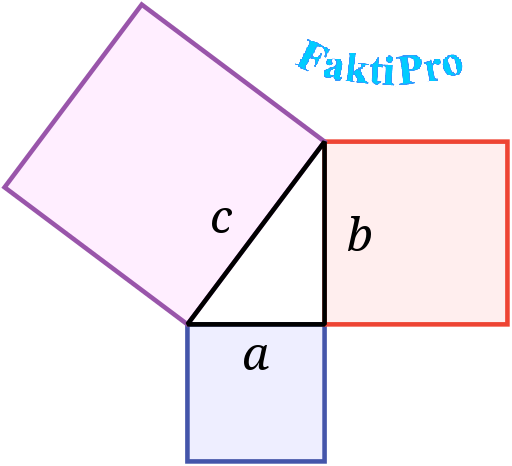
Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. По всей видимости то, что мы называем «теоремой Пифагора», было известно до Пифагора. Античному математику приписывают её доказательство в общем виде. Первоначально «теорема Пифагора» устанавливала соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, а именно «квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах».
Важную роль в структуре мироздания, по мнению пифагорейцев, играют фигурные числа. Об этом классе чисел много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским, которые установили ряд зависимостей между фигурными числами разных размерностей. Пифагорейская нумерология оказала большое влияние на Кеплера.

В музыке
Согласно легенде, Пифагор первым обнаружил, что музыкальные ноты можно перевести в математические уравнения. Одна из легенд утверждает, что Пифагор зашёл в кузницу и начал пробовать каждый из молотков. В результате он понял, что звук прямо пропорционален размеру молотка, из чего сделал вывод, что в основе музыки лежит математика.

Сама по себе легенда, с точки зрения музыкантов, ложна, так как музыкальные интервалы зависят от длины струны, а не веса молотка. Как бы то ни было, открытые Пифагором и/или его последователями музыкальные соотношения пифагорейцами воспринимались в строго математическом смысле.

Литература
Идея Пифагора о том, что мир состоит из чисел, повлияла на творчество Данте Алигьери. Итальянский писатель восемь раз упоминает античного философа в своих трудах. Литературоведы считают, что «Божественная комедия» наполнена символизмом чисел.

Трансценденталисты считали античные жизнеописания Пифагора руководствами образцовой жизни. Генри Торо впечатлили жизнеописание Пифагора Ямвлиха и «Золотые стихи». Его главный труд «Уолден, или Жизнь в лесу» наполнил идеями пифагореизма о гармонии сфер.
Исаак Ньютон
Следующим о ком пойдет рассказ будет Ньютон. Возможно будут те, кто скажет что о нем не чего говорить. Он ведь физик. Однако он очень известен в математике, механики и астрономии, а также в сфере математического анализа.

Исаак Ньютон – многие думают, что он был известен только в области физики. Однако это не так. Он очень известен и в математике. Один из его основных трудов касался математики. Назывался он: «Математические начала натуральной философии».
Автор фундаментального труда «Математические начала натуральной философии». Благодаря математике ученый обнаружил и обнародовал законы движения и закон всемирного тяготения, сформировавшие господствующую научную точку зрения вплоть до появления общей теории относительности.

Вот еще факт влияния математики на жизнь человека. Ньютон использовал свое математическое описание гравитации для строгого вывода эмпирических кеплеровских законов движения планет, а также для построения научной теории приливов, прецессии равноденствий и других явлений. Труд Ньютона устранил всякие сомнения в гелиоцентричности Солнечной системы и продемонстрировал, что движение объектов на Земле и небесных тел можно объяснить одними и теми же физическими принципами. Вывод Ньютона о том, что Земля представляет собой сплюснутый сфероид, впоследствии был подтвержден геодезическими измерениями Мопертюи, ла Кондамина и других, убедивших большинство европейских ученых в превосходстве ньютоновской механики над более ранними системами.

В математике Ньютон разработал дифференциальное и интегральное исчисления, мощный вычислительный метод нахождения корней функций, классифицировал большинство кубических алгебраических кривых, продвинул теорию степенных рядов, обобщил биномиальную теорему на нецелые показатели.
«Математические начала натуральной философии» (лат. Philosophiae Naturalis Principia Mathematica) как по физическому, так и по математическому уровню труд Ньютона качественно превосходит работы всех его предшественников. В нём отсутствует аристотелева или декартова метафизика, с её туманными рассуждениями и неясно сформулированными, часто надуманными «первопричинами» природных явлений. Ньютон, например, не провозглашает, что в природе действует закон тяготения, он строго доказывает этот факт, исходя из наблюдаемой картины движения планет и их спутников. Это все благодаря математике.

Метод Ньютона ‒ создание модели явления, «не измышляя гипотез», а потом уже, если данных достаточно, поиск его причин. Такой подход, начало которому было положено Галилеем, означал конец старой физики. Качественное описание природы уступило место количественному — значительную часть книги занимают расчёты, чертежи и таблицы.
Слабым местом теории тяготения Ньютона, по мнению многих учёных того времени, было отсутствие объяснения природы этой силы. Ньютон изложил только математический аппарат, оставив открытыми вопросы о причине тяготения и его материальном носителе. Для научной общественности, воспитанной на философии Декарта, это был непривычный и вызывающий подход, и лишь триумфальный успех небесной механики в XVIII веке заставил физиков временно примириться с ньютоновской теорией. Физические основы тяготения прояснились только спустя более чем два века, с появлением Общей теории относительности. То есть математика позволила Ньютону опередить время на более чем два века.

Математический аппарат и общую структуру Ньютон построил максимально близкими к признанному его современниками стандарту научной строгости — «Началам» Евклида. Математический анализ он сознательно почти нигде не использовал — применение новых, непривычных методов поставило бы под угрозу доверие к изложенным результатам. Эта осторожность, однако, обесценила ньютоновский метод изложения для следующих поколений читателей. Книга Ньютона была первой работой по новой физике и одновременно одним из последних серьёзных трудов, использующих старые методы математического исследования. Все последователи Ньютона уже использовали созданные им мощные методы математического анализа. Крупнейшими непосредственными продолжателями дела Ньютона стали Д’Аламбер, Эйлер, Лаплас, Клеро и Лагранж.
Первые математические открытия Ньютон сделал ещё в студенческие годы: классификация алгебраических кривых 3-го порядка (кривые 2-го порядка исследовал Ферма) и биномиальное разложение произвольной (не обязательно целой) степени, с которого начинается ньютоновская теория бесконечных рядов — нового и мощнейшего инструмента анализа. Разложение в ряд Ньютон считал основным и общим методом анализа функций, и в этом деле достиг вершин мастерства. Он использовал ряды для вычисления таблиц, решения уравнений (в том числе дифференциальных), исследования поведения функций. Ньютон сумел получить разложение для всех стандартных на тот момент функций.
Ньютон разработал дифференциальное и интегральное исчисление одновременно с Г. Лейбницем и независимо от него. До Ньютона действия с бесконечно малыми не были увязаны в единую теорию и носили характер разрозненных остроумных приёмов. Создание системного математического анализа сводит решение соответствующих задач, в значительной степени, до технического уровня. Появился комплекс понятий, операций и символов, ставший отправной базой дальнейшего развития математики. Следующий, XVIII век, стал веком бурного и чрезвычайно успешного развития аналитических методов.
Возможно, Ньютон пришёл к идее анализа через разностные методы, которыми много и глубоко занимался. Правда, в своих «Началах» Ньютон почти не использовал бесконечно малых, придерживаясь античных (геометрических) приёмов доказательства, но в других трудах применял их свободно. Отправной точкой для дифференциального и интегрального исчисления были работы Кавальери и особенно Ферма, который уже умел (для алгебраических кривых) проводить касательные, находить экстремумы, точки перегиба и кривизну кривой, вычислять площадь её сегмента. Из других предшественников сам Ньютон называл Валлиса, Барроу и шотландского учёного Джеймса Грегори. Понятия функции ещё не было, все кривые он трактовал кинематически как траектории движущейся точки. В любом случае математика существенно сказалась на жизни ученного.
Уже будучи студентом, Ньютон понял, что дифференцирование и интегрирование — взаимно обратные операции. Эта основная теорема анализа уже более или менее ясно вырисовывалась в работах Торричелли, Грегори и Барроу, однако лишь Ньютон понял, что на этой основе можно получить не только отдельные открытия, но мощное системное исчисление, подобное алгебре, с чёткими правилами и гигантскими возможностями.
Ньютон почти 30 лет не заботился о публикации своего варианта анализа, хотя в письмах охотно делится многим из достигнутого. Тем временем вариант Лейбница широко и открыто распространяется по Европе с 1676 года. Лишь в 1693 году появляется первое изложение варианта Ньютона — в виде приложения к «Трактату по алгебре» Валлиса. Приходится признать, что терминология и символика Ньютона по сравнению с лейбницевской довольно неуклюжи: флюксия (производная), флюэнта (первообразная), момент величины (дифференциал) и т. п. Сохранились в математике только ньютоновское обозначение «o» для бесконечно малой dt, да ещё точка над буквой как символ производной по времени.
Достаточно полное изложение принципов анализа Ньютон опубликовал только в работе «О квадратуре кривых» (1704), приложенной к его монографии «Оптика». Почти весь изложенный материал был готов ещё в 1670—1680-е годы, но лишь теперь Грегори и Галлей уговорили Ньютона издать работу, которая, с опозданием на 40 лет, стала первым печатным трудом Ньютона по анализу. Здесь у Ньютона появляются производные высших порядков, найдены значения интегралов разнообразных рациональных и иррациональных функций, приведены примеры решения дифференциальных уравнений 1-го порядка.
В 1707 году вышла книга «Универсальная арифметика». В ней приведены разнообразные численные методы. Ньютон всегда уделял большое внимание приближённому решению уравнений. Знаменитый метод Ньютона позволял находить корни уравнений с немыслимой ранее скоростью и точностью (опубликован в «Алгебре» Валлиса, 1685). Современный вид итерационному методу Ньютона придал Джозеф Рафсон (1690).

В 1711 году наконец был напечатан, спустя 40 лет, «Анализ с помощью уравнений с бесконечным числом членов». В этом труде Ньютон с одинаковой лёгкостью исследует как алгебраические, так и «механические» кривые (циклоиду, квадратрису). Появляются частные производные. В этом же году выходит «Метод разностей», где Ньютон предложил интерполяционную формулу для проведении через (n + 1) данные точки с равноотстоящими или неравноотстоящими абсциссами многочлена n-го порядка. Это разностный аналог формулы Тейлора.
В 1736 году был посмертно издан итоговый труд «Метод флюксий и бесконечных рядов», существенно продвинутый по сравнению с «Анализом с помощью уравнений». В нём приводятся многочисленные примеры отыскания экстремумов, касательных и нормалей, вычисления радиусов и центров кривизны в декартовых и полярных координатах, отыскания точек перегиба и т. п. В этом же сочинении произведены квадратуры и спрямления разнообразных кривых.
Ньютон не только достаточно полно разработал анализ, но и сделал попытку строго обосновать его принципы. Если Лейбниц склонялся к идее актуальных бесконечно малых, то Ньютон предложил (в «Началах») общую теорию предельных переходов, которую несколько витиевато назвал «метод первых и последних отношений». Используется именно современный термин «предел» (лат. limes), хотя внятное описание сущности этого термина отсутствует, подразумевая интуитивное понимание. Теория пределов изложена в 11 леммах книги I «Начал»; одна лемма есть также в книге II. Арифметика пределов отсутствует, нет доказательства единственности предела, не выявлена его связь с бесконечно малыми. Однако Ньютон справедливо указывает на большую строгость такого подхода по сравнению с «грубым» методом неделимых. Тем не менее в книге II, введя «моменты» (дифференциалы), Ньютон вновь запутывает дело, фактически рассматривая их как актуальные бесконечно малые.
Декарт
Нельзя не вспомнить о легендарном французе Декарте, который ввел понятия переменной величины. С его открытиями сталкивался каждый из нас. К ним можно отнести систему координат.
В 1637 году вышел в свет главный философско-математический труд Декарта, «Рассуждение о методе» (полное название: «Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках»). В приложении «Геометрия» к этой книге излагались аналитическая геометрия, многочисленные результаты в алгебре и геометрии, в другом приложении — открытия в оптике (в том числе — правильная формулировка закона преломления света) и многое другое. Все его утверждения имели математическое подтверждение.

Особо следует отметить переработанную им математическую символику, с этого момента близкую к современной. Коэффициенты он обозначал a, b, c…, а неизвестные — x, y, z. Натуральный показатель степени принял современный вид (дробные и отрицательные утвердились благодаря Ньютону). Появилась черта над подкоренным выражением. Уравнения приводятся к канонической форме (в правой части — ноль).
Символическую алгебру Декарт называл «Всеобщей математикой», и писал, что она должна объяснить «всё относящееся к порядку и мере».
Создание аналитической геометрии позволило перевести исследование геометрических свойств кривых и тел на алгебраический язык, то есть анализировать уравнение кривой в некоторой системе координат. Этот перевод имел тот недостаток, что теперь надо было аккуратно определять подлинные геометрические свойства, не зависящие от системы координат (инварианты). Однако достоинства нового метода были исключительно велики, и Декарт продемонстрировал их в той же книге, открыв множество положений, неизвестных древним и современным ему математикам.
В «Геометрии» были даны методы решения алгебраических уравнений (в том числе геометрические и механические), классификация алгебраических кривых. Новый способ задания кривой — с помощью уравнения — был решающим шагом к понятию функции. Декарт формулирует точное «правило знаков» для определения числа положительных корней уравнения, хотя и не доказывает его.
Декарт исследовал алгебраические функции (многочлены), а также ряд «механических» (спирали, циклоида). Для трансцендентных функций, по мнению Декарта, общего метода исследования не существует.

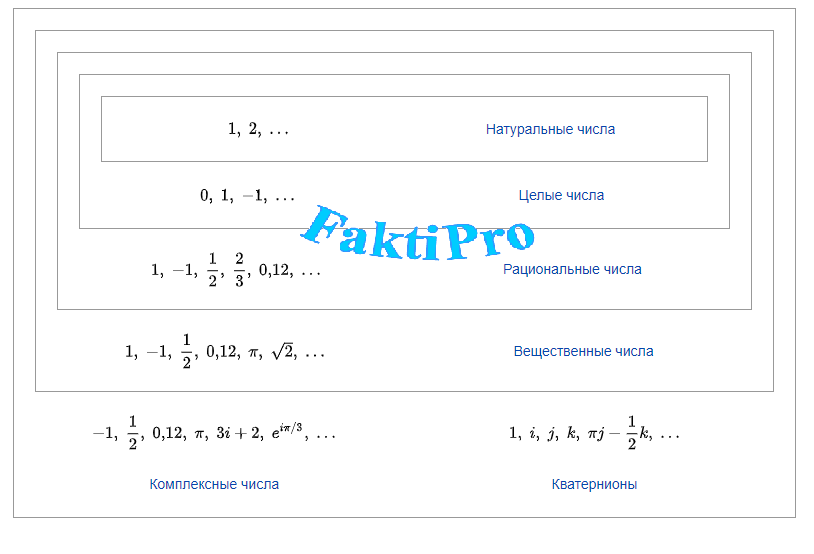
Комплексные числа ещё не рассматривались Декартом на равных правах с вещественными, однако он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней многочлена равно его степени. Отрицательные корни Декарт по традиции именовал ложными, однако объединял их с положительными термином действительные числа, отделяя от мнимых (комплексных). Этот термин вошёл в математику. Впрочем, Декарт проявил некоторую непоследовательность: коэффициенты a, b, c… у него считались положительными, а случай неизвестного знака специально отмечался многоточием слева.
Все неотрицательные вещественные числа, не исключая иррациональные, рассматриваются Декартом как равноправные; они определяются как отношения длины некоторого отрезка к эталону длины. Позже аналогичное определение числа приняли Ньютон и Эйлер. Декарт пока ещё не отделяет алгебру от геометрии, хотя и меняет их приоритеты; решение уравнения он понимает как построение отрезка с длиной, равной корню уравнения. Этот анахронизм был вскоре отброшен его учениками, прежде всего — английскими, для которых геометрические построения — чисто вспомогательный приём.
«Геометрия» сразу сделала Декарта признанным авторитетом в математике и оптике. Издана она была на французском, а не на латинском языке. «Геометрия» была, однако, тут же переведена на латинский и неоднократно издавалась отдельно, разрастаясь от комментариев и став настольной книгой европейских учёных. Труды математиков второй половины XVII века отражают сильнейшее влияние Декарта.

Алан Тьюринг
Теперь давайте еще поговорим о том самом математике, который смог взломать легендарную машину «Энигма». Да, да, да ‒ это Алан Тьюринг, статуя которого есть в Блечли парке. Главное достижение Алана считается разработка метода взлома немецкого кода. Его изобретение помогало читать практически все сообщения немецких войск. Именно из-за этого он считается основателем современного криптоанализа.
Интересные факты про легендарного математика Алана Тьюринга переплетаются с математикой. Он был знаменит и известен благодаря своему гениальному уму, развить который удалось в том числе и благодаря увлечению математикой.
Рассмотрим интересные факты из его жизни. Учился он в школе для аристократов. Успехи в учебе были довольно посредственными. Он увлекался только математикой. И по этому предмету он был впереди всех. Еще он очень любил спорт. Должен был принимать участие в Олимпиаде. Но, участие принять не смог. Причиной этому стала травма ноги.
Тьюринг проявлял незаурядные способности. Он решал сложные математические задачи в 1927 году, несмотря на то, что ему не преподавали даже основ математического анализа. В 1928 году, в возрасте 16 лет, Тьюринг ознакомился с работой Эйнштейна, в которой ему удалось разобраться до такой степени, что он смог экстраполировать из текста сомнения Эйнштейна относительно выполнимости Законов Ньютона, которые не были высказаны в статье в явном виде.

Джон Нэш
Следующим математиком, о котором пойдет рассказ станет тот, кто получил Нобелескую премию. Пусть это произошло в другой сфере, но все же. Его вклад в развитие науки тоже был хороший. Им стал – Джон Нэш-младший. Его можно отнести к тем людям, которые умеют находить выход из самых сложных ситуаций. И самое главное обернуть их себе в пользу. Будущий ученый не всегда был хорошим и примерным студентом. На занятиях он был нечастый гость. В молодые годы, он считал, что математика только и делает, что снижает исследовательскую оригинальность.
У Джона оказалась сложная судьба. Он страдал параноидальной шизофренией. Ученый ходил на прием к психиатору и лежал в клинике. А самым главным его достижением стало то, что он смог сам побороть эти симптомы. И вернулся к деятельности. Помогла ему в этом в том числе и математика.
Погиб он вместе со своей женой в автомобильной аварии. Такси, в котором они ехали, врезалось в заграждение. Произошло это в 2015 году. Ему было 86 лет. Математика позволила ему сохранить хороший ум до конца жизни.
Джон Форбс Нэш-младший ‒ американский математик, работавший в области теории игр, дифференциальной геометрии и изучения уравнений в частных производных. Его теории широко используются в экономике. Математика очень часто тесно переплетается с экономикой и бухгалтерским учетом.
В 2015 году Джон Нэш получил высшую награду по математике — Абелевскую премию — за вклад в теорию нелинейных дифференциальных уравнений. Джон Форбс Нэш стал первым человеком в мире, который был удостоен обеих престижных наград — как Нобелевской, так и Абелевской премий.

Софья Ковалевская
В конце хотелось бы затронуть факты истории математики, связанные со слабым полом. женщин не так много в математике, однако немного наскрести фактов про девушек можно.
Одной из первых женщин в математике стала Софья Ковалевская. Возможно самое печальное, что ей пришлось покинуть страну. Причина этого довольна проста ‒ поиски лучшей жизни после самоубийства мужа. Ей ничего не осталось как покинуть страну. В результате это помогло стать ей довольно известной и стать лауреатом одной из известных премий.

В 1888 году Ковалевская стала лауреатом премии Бордена Парижской академии наук за открытие третьего классического случая разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки. Вторая работа на ту же тему в 1889 году была отмечена премией Шведской академии наук, и Ковалевская была избрана членом-корреспондентом на физико-математическом отделении Российской академии наук.
Наиболее важные исследования относятся к теории вращения твёрдого тела. Ковалевская открыла третий классический случай разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки. Этим продвинула вперёд решение задачи, начатое Леонардом Эйлером и Ж. Л. Лагранжем.
Софья Ковалевская доказала существование аналитического решения задачи Коши для систем дифференциальных уравнений с частными производными, исследовала задачу Лапласа о равновесии кольца Сатурна, получила второе приближение.
Она решила задачу о приведении некоторого класса абелевых интегралов третьего ранга к эллиптическим интегралам. Работала также в области теории потенциала, математической физики, небесной механики.
В 1889 году Софья Ковалевская получила большую премию Парижской академии за исследование о вращении тяжёлого несимметричного волчка.

Заключение
Математика – это та самая удивительная наука. Она имеет множество примеров влияния на жизнь человека. Нужно лишь посмотреть на это с другой стороны и проявить каплю любопытства. И вот тогда этот (как многие считают) скучный предмет заиграет чем-то новым. Читайте интересные факты про математиков, а также факты из жизни математиков на портале ФактыПро и узнавайте много нового. Пишите в комментарии все самое интересное, ведь факты о математике можно перечислять очень долго.








